Mi az a CoCoA?

Nagyon nagy egész számok

Egy 32-bites számítógépen a legnagyobb gépi egész 2^32-1, de a GMP könyvtárnak hála, CoCoA-ban egészen 2^300000 nagyságú számokig lehet dolgozni.

2^32-1;

4294967295

2^64-1;

18446744073709551615

Racionális számok

CoCoA pontosan kezeli a törteket, sohasem használ közelítést. Így például 1/3 és 0.3333333333333 nem egyenlõek.

(1/3) * 3;

0.3333333333333 * 3;

9999999999999/10000000000000

Polinomok

CoCoA elsõsorban polinomokkal kapcsolatos számolások elvégzésére készült. Tud többek között szorozni, osztani, faktorizálni.

(x-y)^2 * (x^4-4*z^4) / (x^2+2*z^2);

x^4 -2*x^3*y +x^2*y^2 -2*x^2*z^2 +4*x*y*z^2 -2*y^2*z^2

Factor(x^4 -2*x^3*y +x^2*y^2 -2*x^2*z^2 +4*x*y*z^2 -2*y^2*z^2);

record[
  RemainingFactor := 1,
  factors := [x^2 -2*z^2,  x -y],
  multiplicities := [1,  2]]
]

Lineáris egyenletrendszerek

CoCoA meg tud oldani lineáris egyenletrendszereket. Az f = c egyenleteket f - c alakban kell megadni. Polinomiális egyenletrendszereket is meg tud oldani, de ez valamivel bonyolultabb, késõbb még vissztérünk rá. Most megoldjuk a következõ rendszert:

x-y+z	=2
3x-z	=-6
x+y	=1

System := ideal(x-y+z-2, 3*x-z+6, x+y-1);
ReducedGBasis(System);

[x +3/5,  y -8/5,  z -21/5]

Ezek szerint a megoldás (z=21/5, x=-3/5, y=8/5).

Nemnegatív egész megoldások

Hogyan keressük meg az alábbi egyenlet nemnegatív egész megoldásait?

3x - 4y + 7z	=2
2x - 2y + 5z	=10

M := mat([[3, -4, 7, -2], [2, -2, 5, -10]]);
H := HilbertBasisKer(M);
L := [h In H | h[4] <= 1];
L;

[[0, 10, 6, 1], [6, 11, 4, 1], [12, 12, 2, 1], [18, 13, 0, 1]]

A kapott eredmény azt mutatja, hogy pontosan négy megoldás van: (0, 10, 6), (6, 11, 4), (12, 12, 2), (18, 13, 0).

Egy logika példa

A azt mondja, hogy B hazudik.
B azt állítja, hogy C hazudik.
C szerint A és B is hazudik.
Akkor most ki mond igazat és ki nem?
A kérdés megoldása céljából legyen 1 az IGAZ és 0 a HAMIS a ZZ/(2) test felett.

use ZZ/(2)[a,b,c];
I1 := ideal(a, b-1);
I2 := ideal(a-1, b);
A := intersect(I1, I2);
I3 := ideal(b, c-1);
I4 := ideal(b-1, c);
B := intersect(I3, I4);
I5 := ideal(a, b, c-1);
I6 := ideal(b-1, a, c);
I7 := ideal(b, a-1, c);
I8 := ideal(b-1, a-1, c);
C := IntersectList([I5, I6, I7, I8]);
ReducedGBasis(A + B + C);

[b +1,  a,  c]

Egyetlen megoldása van az egyenletrendszernek. A megoldás azt mutatja, hogy A és C hazudik, B igazat mond.

Térkép színezés

Kiszínezhetõek az alábbi térképen az országok úgy, hogy bármely két szomszédos ország különbözõ színû legyen?

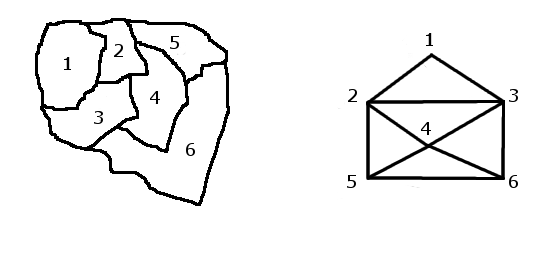
use P ::= ZZ/(3)[x[1..6]];
define F(X)  return X*(X-1)*(X+1);  enddefine;
VerticesEq := [ F(x[i]) | i in 1..6 ];
edges := [[1,2],[1,3],  [2,3],[2,4],[2,5],  [3,4],[3,6],
          [4,5],[4,6],  [5,6]];
EdgesEq := [ (F(x[edge[1]])-F(x[edge[2]]))/(x[edge[1]]-x[edge[2]])
                  |  edge in edges ];
I := ideal(VerticesEq) + ideal(EdgesEq) + ideal(x[1]-1, x[2]);
ReducedGBasis(I);

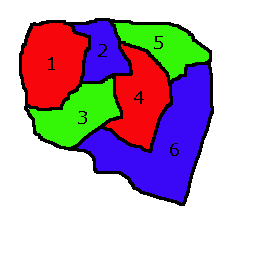
[x[2],  x[1] -1,  x[3] +1,  x[4] -1,  x[6],  x[5] +1]

A megoldás azt mutatja, hogy a fenti térképhez van megfelelõ színezés. Például ha 0 kék, 1 piros és -1 zöld, akkor az eredmény [1. ország = piros; 2. ország = kék; 3. ország = zöld; 4. ország = piros; 5. ország = zöld; 6. ország = kék]

Heron-képlet

Kifejezhetõ a háromszög területe három oldalának hosszával?

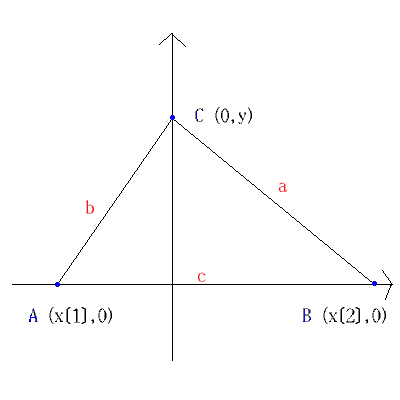
use QQ[x[1..2],y,a,b,c,s];
A := [x[1], 0];
B := [x[2], 0];
C := [ 0,   y];
Hp := ideal(a^2 - (x[2]^2+y^2),  b^2 - (x[1]^2+y^2),
            c   - (x[2]-x[1]),   2*s - c*y);
E := elim(x[1]..y, Hp);
f := monic(gens(E)[1]);
f;

a^4 -2*a^2*b^2 +b^4 -2*a^2*c^2 -2*b^2*c^2 +c^4 +16*s^2

factor(f - 16*s^2);

record[
  RemainingFactor := 1,
  factors := [a +b -c,  a -b +c,  a +b +c,  a -b -c],
  multiplicities := [1,  1,  1,  1]
]

Azt kaptuk, hogy s^2 = -(1/16)(a+b+c)(a+b-c)(a-b+c)(a-b-c). Ezek szerint az a, b, c oldalhosszú háromszög területe p(p-a)(p-b)(p-c), ahol p = 1/2(a+b+c) a kerület fele.