What is CoCoA?

Very Big Integers

The biggest "machine integer" you can use on a 32-bit computer is 2^32-1, but CoCoA, thanks to the powerful GMP library, can even compute numbers as big as 2^300000: try it!

2^32-1;

4294967295

2^64-1;

18446744073709551615

Rational Numbers

CoCoA is very precise with fractions: it never approximates them! So 1/3 is quite different from 0.3333333333333

(1/3) * 3;

0.3333333333333 * 3;

9999999999999/10000000000000

Polynomials

CoCoA is specialized in polynomial computations: it can multiply, divide, factorize, ...

(x-y)^2 * (x^4-4*z^4) / (x^2+2*z^2);

x^4 -2*x^3*y +x^2*y^2 -2*x^2*z^2 +4*x*y*z^2 -2*y^2*z^2

Factor(x^4 -2*x^3*y +x^2*y^2 -2*x^2*z^2 +4*x*y*z^2 -2*y^2*z^2);

record[
  RemainingFactor := 1,
  factors := [x^2 -2*z^2,  x -y],
  multiplicities := [1,  2]]
]

Linear Systems

CoCoA can solve linear systems. You just need to write every equation f = c as the polynomial

f -
   c

. CoCoA can also solve polynomial systems, but this is a bit more difficult and we'll see it later. Now we solve

x-y+z	=2
3x-z	=-6
x+y	=1

System := ideal(x-y+z-2, 3*x-z+6, x+y-1);
ReducedGBasis(System);

[x +3/5,  y -8/5,  z -21/5]

Hence the solution is (z=21/5, x=-3/5, y=8/5)

Non-negative Integer Solutions

Can you find the triples of non-negative integer solutions of the following system?

3x - 4y + 7z	=2
2x - 2y + 5z	=10

M := mat([[3, -4, 7, -2], [2, -2, 5, -10]]);
H := HilbertBasisKer(M);
L := [h In H | h[4] <= 1];
L;

[[0, 10, 6, 1], [6, 11, 4, 1], [12, 12, 2, 1], [18, 13, 0, 1]]

The interpretation is that there are just four solutions: (0, 10, 6), (6, 11, 4), (12, 12, 2), (18, 13, 0).

Logic Example

A says: "B lies."
B says: "C lies."
C says: "A and B lie."
Now, just who is lying here?
To answer this question we code TRUE with 1 and FALSE with 0 in ZZ/(2):

use ZZ/(2)[a,b,c];
I1 := ideal(a, b-1);
I2 := ideal(a-1, b);
A := intersect(I1, I2);
I3 := ideal(b, c-1);
I4 := ideal(b-1, c);
B := intersect(I3, I4);
I5 := ideal(a, b, c-1);
I6 := ideal(b-1, a, c);
I7 := ideal(b, a-1, c);
I8 := ideal(b-1, a-1, c);
C := IntersectList([I5, I6, I7, I8]);
ReducedGBasis(A + B + C);

[b +1,  a,  c]

The unique solution is that A and C were lying, and B was telling the truth.

Geographical Map Coloring

Can the countries on a map be colored with three colors in such a way that no two adjacent countries have the same color?

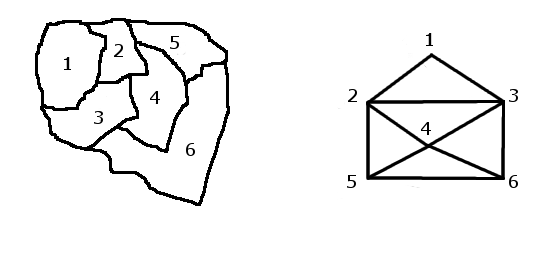
use P ::= ZZ/(3)[x[1..6]];
define F(X)  return X*(X-1)*(X+1);  enddefine;
VerticesEq := [ F(x[i]) | i in 1..6 ];
edges := [[1,2],[1,3],  [2,3],[2,4],[2,5],  [3,4],[3,6],
          [4,5],[4,6],  [5,6]];
EdgesEq := [ (F(x[edge[1]])-F(x[edge[2]]))/(x[edge[1]]-x[edge[2]])
                  |  edge in edges ];
I := ideal(VerticesEq) + ideal(EdgesEq) + ideal(x[1]-1, x[2]);
ReducedGBasis(I);

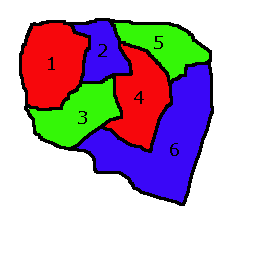
[x[2],  x[1] -1,  x[3] +1,  x[4] -1,  x[6],  x[5] +1]

The interpretation is that there is indeed a coloring in this case. For instance, if 0 means blue, 1 means red, and -1 means green, we get [country 1 = red; country 2 = blue; country 3 = green; country 4 = red; country 5 = green; country 6 = blue]

Heron's Formula

Is it possible to express the area of a triangle as a function of the length of its sides?

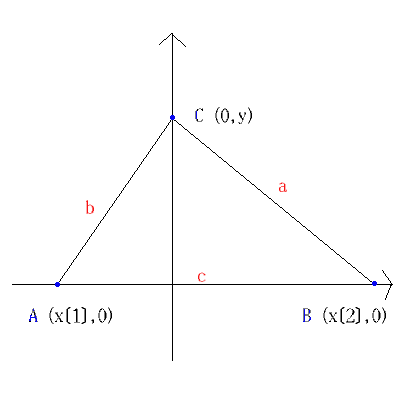
use QQ[x[1..2],y,a,b,c,s];
A := [x[1], 0];
B := [x[2], 0];
C := [ 0,   y];
Hp := ideal(a^2 - (x[2]^2+y^2),  b^2 - (x[1]^2+y^2),
            c   - (x[2]-x[1]),   2*s - c*y);
E := elim(x[1]..y, Hp);
f := monic(gens(E)[1]);
f;

a^4 -2*a^2*b^2 +b^4 -2*a^2*c^2 -2*b^2*c^2 +c^4 +16*s^2

factor(f - 16*s^2);

record[
  RemainingFactor := 1,
  factors := [a +b -c,  a -b +c,  a +b +c,  a -b -c],
  multiplicities := [1,  1,  1,  1]
]

The interpretation is that we have s^2 = -(1/16)(a+b+c)(a+b-c)(a-b+c)(a-b-c). This means that the square of the area of a triangle with sides a, b, c is p(p-a)(p-b)(p-c) where p = 1/2(a+b+c) is the semiperimeter. Hence the answer is YES.